Authors:
(1) Soham De, Google DeepMind and with Equal contributions;
(2) Samuel L. Smith, Google DeepMind and with Equal contributions;
(3) Anushan Fernando, Google DeepMind and with Equal contributions;
(4) Aleksandar Botev, Google DeepMind and with Equal contributions;
(5) George Cristian-Muraru, Google DeepMind and with Equal contributions;
(6) Albert Gu, Work done while at Google DeepMind;
(7) Ruba Haroun, Google DeepMind;
(8) Leonard Berrada, Google DeepMind;
(9) Yutian Chen, Google DeepMind;
(10) Srivatsan Srinivasan, Google DeepMind;
(11) Guillaume Desjardins, Google DeepMind;
(12) Arnaud Doucet, Google DeepMind;
(13) David Budden, Google DeepMind;
(14) Yee Whye Teh, Google DeepMind;
(15) David Budden, Google DeepMind;
(16) Razvan Pascanu, Google DeepMind;
(17) Nando De Freitas, Google DeepMind;
(18) Caglar Gulcehre, Google DeepMind.
Table of Links
3 Recurrent Models Scale as Efficiently as Transformers
3.2. Evaluation on downstream tasks
4.2. Efficient linear recurrences on device
4.3. Training speed on longer sequences
5.1. A simple model of the decode step
6. Long Context Modeling and 6.1. Improving next token prediction with longer contexts
6.2. Copy and retrieval capabilities
8. Conclusion, Acknowledgements, and References
B. Complex-Gated Linear Recurrent Unit (CG-LRU)
C. Model Scale Hyper-Parameters
D. Efficient Linear Recurrences on Device
E. The Local Attention Window Size of Griffin
G. Improving Next Token Prediction with Longer Contexts: Additional Results
H. Additional Details of the Copy and Retrieval Tasks
2. Model Architecture
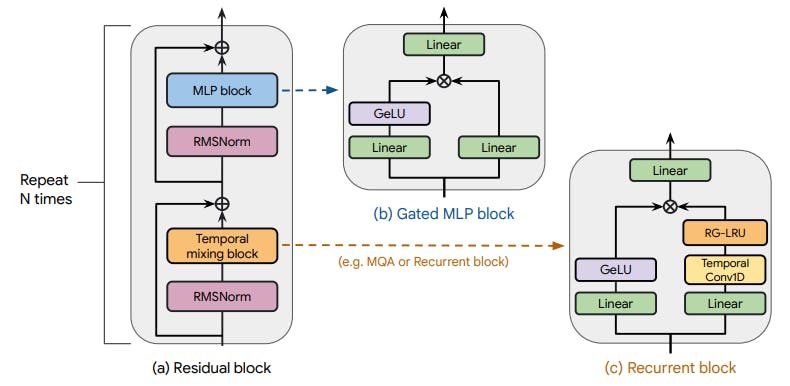
All our models contain the following components: (i) a residual block, (ii) an MLP block, and (iii) a temporal-mixing block. While (i) and (ii) are the same across all models, we consider three temporal mixing blocks: global Multi-Query Attention (MQA), local (sliding-window) MQA and our proposed recurrent block. As part of the recurrent block we use the Real-Gated Linear Recurrent Unit (RG-LRU) – a novel recurrent layer inspired by the Linear Recurrent Unit (Orvieto et al., 2023b).
The residual block, as shown in Figure 2(a), defines the global structure of our models and is inspired by pre-norm Transformers (Xiong et al., 2020). After embedding the input sequence we pass it through 𝑁 such blocks (𝑁 denoting the model depth), and then we apply RMSNorm (Zhang and Sennrich, 2019) to produce the final activations. To compute the token probabilities we apply a final linear layer followed by a softmax. The weights of this layer are shared with the input embedding layer.
2.1. Residual block
The residual block contains two components, applied in order. The first component takes the hidden state 𝑥 and applies an RMSNorm (Zhang and Sennrich, 2019), followed by the temporal-mixing block.
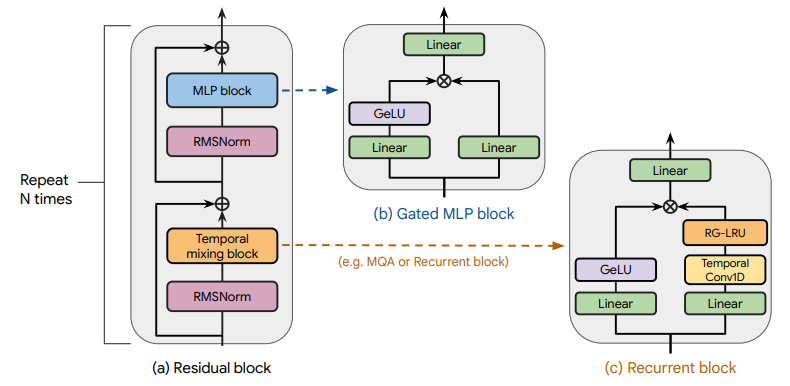
We then merge the output with a skip connection from 𝑥 through addition. Similarly, the second component applies RMSNorm, followed by the MLP block and then merges its output with a skip connection from the input of the RMSNorm. This block is illustrated in Figure 2 (a).
2.2. MLP block
We use a gated MLP block (Dauphin et al., 2017) (illustrated in Figure 2(b)), which creates two branches from its input of dimension 𝐷. We apply a linear layer with output dimension 𝑀𝐷 on each branch, where 𝑀 denotes the expansion factor. For simplicity, we use 𝑀 =3 throughout this work. We apply a GeLU non-linearity (Hendrycks and Gimpel, 2016) on one of the branches before merging them by element-wise multiplication, similar to GeGeLU (Shazeer, 2020). However, in our MLP block, we apply a final linear layer with output dimension 𝐷 on the outputs of the GeGeLU layer.
2.3. Temporal-mixing blocks
The temporal-mixing block is the component of our model that aggregates hidden layer activations at different temporal locations in the sequence. We consider three temporal-mixing blocks: global MQA (Shazeer, 2019), local MQA (Beltagy et al., 2020) and our proposed Recurrent block.

Local sliding window attention One of the key disadvantages of using global attention is that its computational complexity grows quadratically in the sequence length. To address this, several works have started to adopt local attention (Beltagy et al., 2020), also known as sliding window attention. It allows each position to attend only to a fixed number of tokens in the past. This not only reduces the computational FLOPs but also bounds the size of the KV cache to the size of window, making it no longer quadratic in the sequence length. All other details are the same as the global MQA.

2.4. Real-Gated Linear Recurrent Unit (RG-LRU)
Our proposed RG-LRU layer has a simple recurrence inspired by the Linear Recurrent Unit (LRU) (Orvieto et al., 2023b), but incorporates a gating mechanism motivated by the literature on non-linear RNNs, in particular LSTMs (Hochreiter and Schmidhuber, 1997) and GRUs (Chung et al., 2014). The equations describing the layer are as follows:

This paper is available on arxiv under CC BY 4.0 DEED license.
[1] We suggest ablating the use of complex numbers for other modalities and provide more information about the complex-valued version of the RG-LRU layer in Appendix B.