Recurrent Models: Enhancing Latency and Throughput Efficiency

Table of Links

1 Introduction

2 Model Architecture

3 Recurrent Models Scale as Efficiently as Transformers

3.1. Scaling curves

3.2. Evaluation on downstream tasks

4 Training Recurrent Models Efficiently on Device and 4.1. Model parallelism for large scale training

4.2. Efficient linear recurrences on device

4.3. Training speed on longer sequences

5. Inference Speed

5.1. A simple model of the decode step

5.2. Results

6. Long Context Modeling and 6.1. Improving next token prediction with longer contexts

6.2. Copy and retrieval capabilities

7. Related Works

8. Conclusion, Acknowledgements, and References

A. RG-LRU Recurrence Gate

B. Complex-Gated Linear Recurrent Unit (CG-LRU)

C. Model Scale Hyper-Parameters

D. Efficient Linear Recurrences on Device

E. The Local Attention Window Size of Griffin

F. Inference Speeds

G. Improving Next Token Prediction with Longer Contexts: Additional Results

H. Additional Details of the Copy and Retrieval Tasks

5.1. A simple model of the decode step

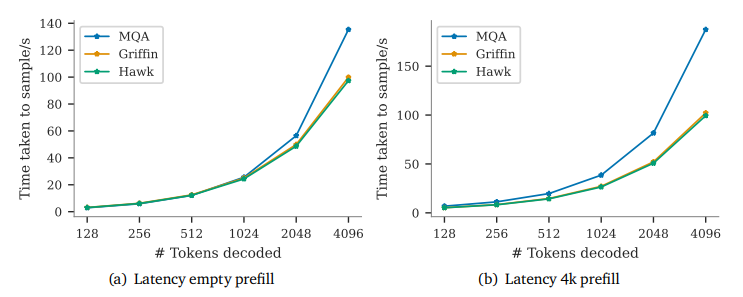
Here, cache size refers to either the size of the KV cache at batch size 1 (for Transformers), or to the size of the recurrent state at batch size 1 (for RNNs).

Cache sizes The difference in cache size relative to model parameters has important implications for sampling efficiency. In recurrent and local attention blocks, parameter loading is the primary bottleneck, (because the cache size is substantially smaller). In contrast, global attention’s KV cache scales with the sequence length 𝑇 and can be comparable to, or even exceed, the size of the model parameters. This introduces considerable overhead when the sequence length 𝑇 is large enough (as shown in F.4). Consequently, an equally sized recurrent model can exhibit substantially lower latency than a Transformer when 𝑇 is large. Note however that as the model size grows the sequence length at which we see latency benefits (where the KV cache size is comparable to parameter size) also increases. It is important to note that, as well as improving latency, having a small recurrent state can also increase the largest batch size that fits in memory on a single device, leading to higher throughput.